New Directions: A Summary of My Research
Enviado por Kasie Coogan el
This summer I have had the opportunity to explore an area of research that was completely unfamiliar to me. My project studied forced colloids in nematic suspensions via Brownian Dynamics simulations. If this sounds totally confusing to you, then you are in the same boat I was in two months ago. Don’t worry, I’ll clue you in on some of the things I learned this summer. A nematic suspension refers to a group of particles that exhibit a particular alignment along an axis. In this case, the suspension models that of a nematic liquid crystal. Due to their ordering, liquid crystals are anisotropic, meaning that their properties are dependent on the direction in which they are measured. Liquid crystals have an ordering that is between that of an isotropic fluid and a crystalline solid. Isotropic fluids contain particles with completely random orientation, while crystals have perfectly ordered particles. For nematic liquid crystals, the particles have uniaxial ordering, in which the particles are aligned along a single axis, known as the nematic vector. You can think of it like people standing in an elevator: almost everyone will be facing forward, with people staggered and slight variations in how squared off they are standing. The other component of this study comes into play with the forced colloid. The addition of the forcing component introduces active motion to the study. Active motion can be induced by a variety of mechanisms and this study looks at the behavior of an active particle in a liquid crystal. Active matter such as bacteria has previously been observed to be influenced by the direction of liquid crystals orientation. My project specifically evaluated the behavior of the colloid as the level of forcing increased and as the direction of forcing relative to the nematic vector was changed. In order to analyze this behavior, the mean square displacement and diffusivity were measured.
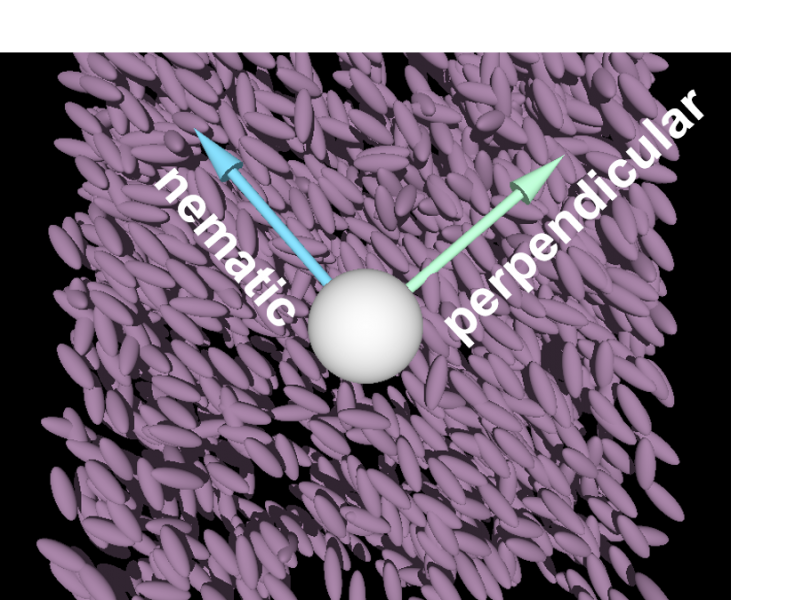
Our method for studying this behavior was through Brownian Dynamics simulations. The simulations consisted of an ellipsoidal particle suspension and a single spherical colloid. The ellipsoids represent the liquid crystal particles. As indicated in the image, the direction of the nematic vector and the perpendicular vector were calculated and the colloid was forced in each direction. The level of forcing applied to the colloid was implemented by the Péclet number at values of 0, 10, and 100. We plotted the mean square displacement and calculated the diffusivity for each simulation in both the parallel and perpendicular direction. The nature of the simulations requires a significant amount of time to reach the final time step. Due to the limited time, we were able to produce data only for the initial time period.
The results indicated that motion is dominated in the direction perpendicular to the nematic vector for most cases. When the colloid is forced parallel with a Péclet number of 100, the displacement is greater in the parallel direction and the total displacement is greater than the other cases. This leads us to expect that a larger Péclet number results in increased displacement. The slowest simulation achieved a time of 0.59, while the fastest achieved 1.29. The limited time and data generated does not allow for any conclusive statements to be made regarding the conditions tested. Therefore, the data presented here provides only preliminary results for these simulations. In order to generate significant data, the simulations must reach their final time and additional replicas of each condition must be performed. A larger understanding of the effect of changing the Péclet number can be established by running simulations with a range of Pe=0.1-1000. It will be possible to then pinpoint at what value a change in the Péclet number has a significant effect on the colloid and liquid crystal microstructure.
Further properties of the simulation can also be calculated. An important calculation to characterize the deformation of the microstructure would be to construct a 2-dimensional map of the order parameter and a density profile of the ellipsoid suspension. To make the 2D map, the simulation box will be separated into subunits and the order parameter and particle density will be calculated in each unit. This map can be constructed over multiple time scales to illustrate the degree to which the motion of the colloid destructs the microstructure and the range to which the ellipsoids are affected. It would be possible to determine if varying the Péclet number and forcing direction affects the change in order parameter or density. In addition to those calculations, the pair distribution function can be calculated for ellipsoids in the suspension.
The results generated in this report serve as preliminary findings to be further investigated and applied to future studies. As the behavior of the colloid is characterized, we can look into its effect on the microstructure of the liquid crystal in future project. Since the findings presented here regarding the direction of the colloid are unexpected, this system can also be investigated experimentally to determine if the same behavior is present. This project has established a fundamental starting point from which more studies can be conducted and allow for a more complete understanding of how active motion interacts with liquid crystals.
I have gained so much from this summer from exploring unfamiliar research and having the opportunity to experience life in Madison and Puerto Rico. The opportunity to learn from the expertise of two institutions has been such a valuable addition to this REU program. I am so grateful for the exposure to many different kinds of research and look forward to further contributing to the scientific community.










